[반도체 소자] "Subthreshold Swing, SS 특성 세부정리"

이번 교육에서는 Subthreshold Swing 특성에 대해서 정리하겠습니다. 이번 장은 수식이 많으니 가볍게 보고 넘어가시면 될 것 같습니다.
교육 #1]. MOSFET 전류전압 방정식
우선 Inversion charge density에서 출발하겠습니다.
Channel voltage (Vc), Source voltage (Vs), Drain voltage (Vd), Channel length (x=0~L)

Inversion charge density, Qinv는 gate oxide capacitance에 Vgs, Vt, body back bias, Vsb에 따라 제어가능합니다. Vcs는 source 대비 channel의 전압ㅣ기 때문에 potential x의 함수로 나타낼 수 있습니다. (-)부호는 electron charge 의미. 결과를 보았을 때, body bias가 포함된 항은 이전 교육에서 배웠던 body factor, m으로 나타낼 수 있습니다.
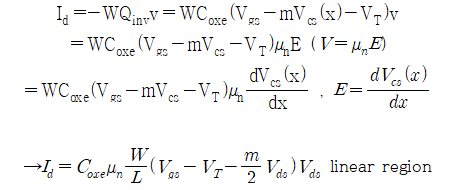
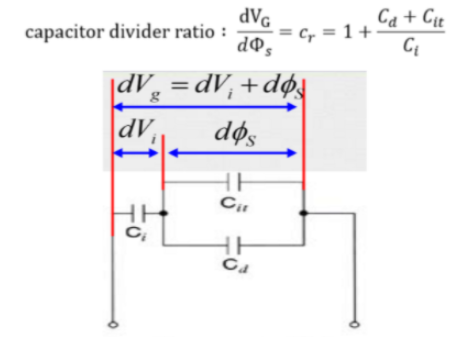
양변을 x에 대해서 적분하면 위와 같은 전류식을 얻을 수 있습니다. 기존 문헌의 보고된 전류방정식과 다른 점은 body factor를 포함하고 있는데, MOSFET을 MOS Capacitor 관점에서 보면, gate oxide, Cox가 있고 Depletion region에 의해 생성되는 Depletion capacitance, Cdep이 존재합니다. 그 외에도 Source/body, Drain/body의 junction capacitance 또한 존재합니다.
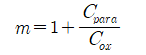
기생캐패시턴스인 Cpara는 'Cpara=Cdep+Cs+Cd'로 depletion capacitance와 source/drain의 junction capacitance로 구성되어 있습니다. 우리가 만약에 gate에 5V를 인가했을 때, 5V가 모두 Channel 형성에 기여하는 것이 아닙니다. Capacitance가 직렬로 연결되어 있기 때문에, Gate voltage는 기생 capacitance에 분배되기 때문에 온전히 gate voltage가 oxide capacitance에 영향을 끼치지 않습니다. gate 제어력을 향상시키기 위해서는 Cpara 값을 낮춰야 하고, 그러기 위해서 oxide thickness를 얇게 가져감으로써 Cox를 향상시키고, shallow junction depth profile 혹은 retrograde body doping profile 등의 기술을 도입하여 Cpara 값을 최소화시켜, body factor 값을 작게 만드는 것입니다. (body factor = 1일 때, 이상적인 경우이며, 이론적인 전류 모델보다 측정값이 작게나오는 이유는 기생캐패시턴스 성분에 의해 body factor가 1이 아니기 때문임)

Output characteristics, 출력특성을 보면 linear 영역과 saturation 영역으로 나눌 수 있습니다. 위와 같이 Drain current, Id를 Vgs로 미분하여 변곡점을 찾습니다. 이때 변화의 극대값을 찾으면 linear 영역에서 saturation 영역으로 전이 되는 point 전압을 saturation voltage, Vdsat라고 표현합니다.
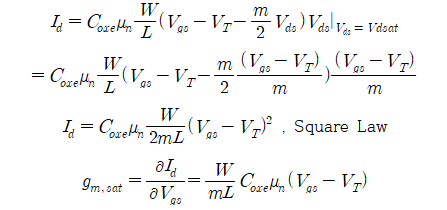
Vds를 saturation voltage, Vdsat로 치환하면, saturation current를 구할 수 있습니다. 학부 과정에서는 body factor=1인 이상적인 전류모델을 적용했습니다. Short channel로 갈수록 channel 길이가 짧아짐에 따라 Drain current, Id가 증가를 기해했지만, channel length가 짧아짐에 따라 기생 capacitance 성분도 증가하게 되면서 body factor 값도 증가하게 되어 소자의 전류 performance는 크게 증가하지 않는 이슈가 발생합니다.
교육 #2]. Subthreshold Current (Diffusion current) 방정식
Subthreshold Swing, SS의 식을 유도해보겠습니다. SS는 Subthreshold region 그래프 기울기의 역수이므로 다음과 같이 표현할 수 있습니다.
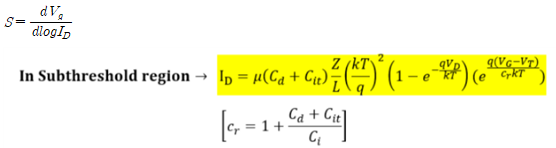
먼저 SS는 게이트전압이 매우 낮은 Subthreshold region에서만 성립하고, 이 영역에서 성립되는 Charge Sheet Model, CSM의 전류식이 이용됩니다. 해당 식은 위와 같고 위 식에서 Vd 값이 적어도 3kT/q보다 크면 exponential 항은 0에 근사하게 되므로 다음과 같은 식을 얻을 수 있습니다.
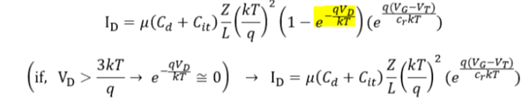
여기서 양변에 자연로그를 취해주면 아래와 같은 식을 얻습니다. (식은 그냥 넘어가세요~)
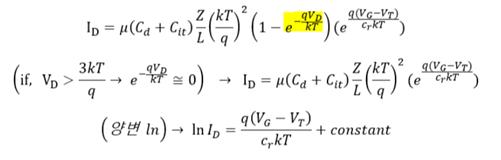
위 식에서 Cr 값은 Capacitor divide ratio이며, 전체 게이트 전압 중 반도체 표면에 얼마나 많은 게이트 전압이 걸리는지 나타내주는 비율을 의미합니다. 즉, 게이트 영향력을 나타내는 지표라고 할 수 있습니다.
이를 이용하여 식을 다시 정리해준 결과는 다음과 같습니다.
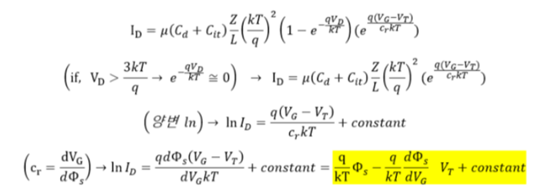
현재 Subthreshold region에서의 전류를 다루고 있기 때문에 반도체 표면에 걸리는 전압 Φs는 게이트 전압에 따라 거의 변하지 않으므로 무시할 수 있습니다.

좌변의 ln(Id)를 log 형태로 바꿔준 후 양변에 d/dVg를 곱해주고나서 계산을 하면 아래와 같습니다.

결국 SS의 식을 위와 같이 구할 수 있으며, S는 Ci 값과 반비례하고 Cd, Cit 값과 비례하는 형태의 식을 가지게 되는 것을 확인할 수 있습니다.
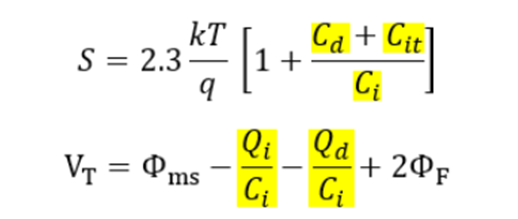
최종적으로 위와 같은 결과를 도출해낼 수 있었습니다. S값이 작아지면 Vt도 함께 작아지는 것을 위 식에서 확인할 수 있습니다. 즉, Depletion region의 capacitance는 depletion region의 전하량과도 비례하며, interface state charge의 영향을 받기 때문에 S가 커지면 Vt도 함께 커지고, S가 작아지면 Vt도 함께 작아지는 것입니다.
가장 이상적인 경우는 Cit가 0이고, Ci가 무한대인 경우입니다. T=300K일 때, 이상적인 S의 값을 구하면 다음과 같습니다.

지금까지 내용을 정리하면 S값은 게이트 전압을 인가했을 때 전류가 얼마나 증가하는지를 나타내는 지표이며, S값이 작으면 Threshold voltage, Vt 또한 작아질 수 있음을 확인했습니다. 그리고 앞선 교육에서 진행했던 Field Effect 전계효과 메커니즘으로 구동하는 소자의 한계를 말씀드렸는데, 위 식에서 60mV의 값을 얻을 수 있습니다.
예를 들면, S값이 80mV/decade에서 20mV/decade로 줄어든다는 것은 무슨 의미인지 이야기해보겠습니다. On current를 형성하기 위한 gate 전압은 threshold voltage, Vt입니다. off current가 있을 때 off current의 10^8 배 하는데 필요한 전압은 몇일까요.
On current / Off current > 10^8 → On current > 10^8 × off current
On current@Vt 이며, off current ×10^8@8SS
→ Threshold voltage, Vt > 8SS
SS는 off current의 전류를 10배 해주기 위해 필요한 전압입니다. 10^8 배 해주기 위해서는 8SS가 필요한 것입니다. 소자가 구동하기 위해서는 문턱전압 Vt > 8SS이어야 하며, SS값이 80mV/decade일 때보다 20mV/decade일 때 더 작은 gate 전압으로 10^8배의 drain current를 얻을 수 있다는 것입니다. 즉, on/off 특성이 매우 우수하며 MOSFET 소자의 전달특성에서 매우 Steep한 기울기가 형성된다는 것을 의미합니다.
교육 #3]. 조금 더 간단하게 Subthreshold Current (Diffusion current) 방정식을 정리하겠습니다.
Subthreshold Swing, SS의 식을 유도해보겠습니다. SS는 Subthreshold region 그래프 기울기의 역수라고 했습니다.
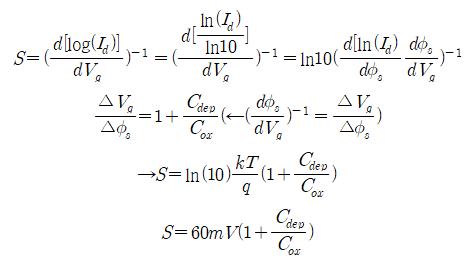
Id-Vgs 전달특성에서 off 상태에서 on 상태로 갈 때, 기울기가 steep 한 것이 매우 이상적입니다. 하지만 MOSFET은 한계를 가지고 있다고 말씀드렸습니다. 이 Slope의 역수를 subthreshold swing, SS라고 합니다. 역함수, 미분, 전압 인가, 어쩌구 저쩌구 교육#2를 따라오다 보면 위와 같은 식을 얻을 수 있습니다. ln10은 2.5xxxx, k는 볼츠만 상수, kT=300K → 26mV 이기에, 계산하면 2.5×26 하면 60mV가 유도됩니다. 즉, 우리가 아무리 소자를 잘 만들어도 기판은 p-type이기에 소수캐리어인 전자가 채널에 많지 않습니다. 그에 반해 source는 n+doping으로 채널과 비교했을 때, 전자가 무수히 많고 채널 쪽으로 캐리어가 확산해서 들어가게 됩니다.
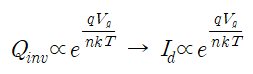
그렇기에 Linear 영역에서는 캐리어의 diffusion 메커니즘이 전류특성에 기인하기에 위와 같은 식을 따르게 됩니다. saturation 영역은 전계에 의한 드리프트 성분이 지배적이기에 아래와 같은 식을 따르는 것입니다.

소자에 인가하는 전압으로 Drift 성분은 충분히 제어가 가능하나, Diffusion 성분은 전류성분이 전압과 상관없이 오로지 확산에 의해 결정되기 때문에 제어하기가 매우 까다롭습니다. 그래서 diffusion current가 주요 성분인 subthreshold region의 전류를 제어하는 것이 큰 이슈인 것입니다.
오랜만에 MOSFET 다시 공부하니 정말 재미있네요.
오늘 하루도 고생 많으셨습니다.
From. 교관 홍딴딴